이번주는 파이썬 시계열 예측 관련 내용이었다.
통계 내용도 많이 나오고 양이 많아서 사실 정해진 진도를 못 따라가긴 했지만 이번 주에 배운 내용을 간략하게 정리해보려고 한다.

Statsmodels
- 시계열 예측에 자주 쓰이는 라이브러리
- 다양한 통계 모형의 추정과 통계 검정, 통계적 데이터 탐색 등을 다루는 클래스와 함수를 제공하는 모듈
시계열 데이터의 속성
1. 추세 : 시계열 데이터는 경향성을 가진다. 시계열 데이터는 어떤 방향으로든 추세를 가진다.
- Upward : 위로 가는 추세
- Horizontal/Stationary : 수평방향, 변하지 않는 추세
- Downward : 아래로 가는 추세
2. 계절성 : 주기적으로 반복적인 추세, 주기가 매우 뚜렷하게 보인다면 계절성.
ex. 매 겨울마다 증가, 매 여름마다 감소
3. 순환 : Cyclical, 반복성이 없는 순환 요소
Hodrick-Prescott filter 호드릭-프레스콧 필터
yt=τt+ct
데이터의 추세 요소와 순환 요소를 찾아 분해.
이 두 요소는 2차 손실 함수를 최소화하는 값으로 결정
* 2차 손실 함수
minτ(∑t=1T(yt−τt)2+λ∑t=2T−1((τt+1−τt)−(τt−τt−1))2)
* λ : 평활화 계수, 추세요소의 증가율 변동폭 조정
분기별 데이터에서는 λ = 1600, 연간 데이터에서는 λ = 6.25, 월간 데이터에서는 λ = 129,600 추천
# 호드릭 프레스콧 필터
from statsmodels.tsa.filters.hp_filter import hpfilter
# 리턴값은 튜플, 두 값을 리턴함 / 순환요소, 추세요소 반환
gdp_cycle, gdp_trend = hpfilter(df['realgdp'], lamb =1600)
type(gdp_trend) # 형태는 시리즈 : pandas.core.series.Series
# 추세요소를 df의 새로운 열로 추가하기
df['trend'] = gdp_trend
# 그래프 그리기
df['trend'].plot()
# 추세 요소랑 realgdp랑 같이 그려보기
df[['realgdp','trend']].plot()
2008년 대불황 이후에 내용만 확대해서 보기
# 2008년 이후의 대불황같이 특정 기간만 확대하기
df[['realgdp','trend']]['2005-01-01':].plot()
# 대불황 이후 몇 년간 추세를 따르지 않는다. (하락 추세)
2008년 대불황 이후 실제 gdp는 추세를 따르지 않고 하락했음.
ETS 분해 (E : Error, T : Trend, S : Seasonality)
* ETS Models
- 지수평활법, ETS분해, 추세모형과 같이 다양한 여러 모델들을 포함하는 일반적 표현
- E,T,S 세가지 요소를 사용해서 데이터를 평활화
* ETS 모델의 종류
- 덧셈 모델 : 추세가 선형에 더 가깝고 계절성이 일정해보일 때 적합
- 곰셉 모델 : 추세가 비선형적으로 증가/감소할 때 적합
from statsmodels.tsa.seasonal import seasonal_decompose
# ETS분해 곱셈모델 사용
result = seasonal_decompose(airline['Thousands of Passengers'], model = 'multiplicative')
result.trend.plot()
result.seasonal.plot()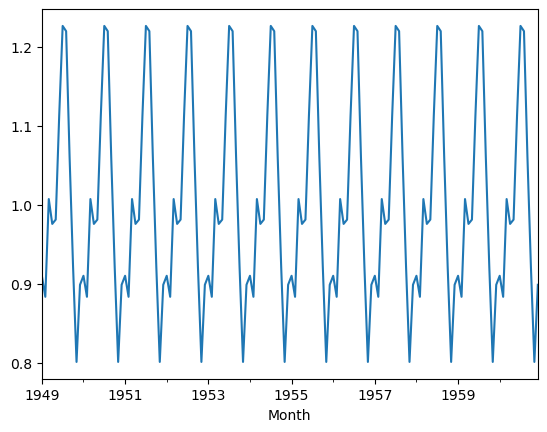
# 잔차
result.resid.plot()
from pylab import rcParams
rcParams['figure.figsize'] = (12,7)
result.plot();
추세 요소 : 데이터 포인트의 전반적인 상승 혹은 하강세를 보여줌.
계절 요소 : 계절성 요소들을 직선화한 것 / 즉 추세 요소를 제거한 것
잔차 요소 : 추세나 계절성으로 설명되지 않는 것들을 나타냄, 어디에 노이즈가 많은지 혹은 그렇지 않은지 나타내는 역할도 함.
EWMA Models (Exponentially-Weighted Moving Average)
* 단순 이동 평균의 문제점
- 전체 모델이 같은 이동 평균 기간으로 제한됨.
- 데이터 하나에 대해 하나의 이동 평균 기간 밖에 적용할 수 없음.
- 평균을 함으로 인해서 원래 데이터의 극대값과 극소값에 미치지 못함.
- 적절한 이동 평균 기간을 찾는 것은 어려움.
* EWMA : 지수 가동 이동 평균, 단순 이동 평균의 단점을 보완.
- 최근의 값들에 가중치를 적용함으로써 단순 이동 평균에서의 시차 효과를 감소시킬 수 있음.
- 가장 최근의 값에 적용되는 가중치는 매개변수에 의해 결정, 이동 평균 기간에 따라서도 변화함.
span : N-일 지수 가중 이동 평균
# 지수 가중 이동 평균
airline['EWMA-12'] = airline['Thousands of Passengers'].ewm(span = 12).mean()
airline[['Thousands of Passengers', 'EWMA-12']].plot()
# 계절성 추세가 시작부분에서 끝 부분으로 갈수록 더 명확하게 보임.

홀트-윈터스 계절성 기법
- EWMA 지수 가중 이동 평균은 계절성이나 전반적인 추세를 고려하지는 못함. (지수 평활 시, 알파 하나의 매개변수만 사용하기 때문)
- lt, bt,st 세 식은 각각에 대응하는 평활 매개변수 알파, 베타, 감마를 갖는다.
* 계절성 요소의 성질에 따라 두 가지로 다룸.
- 덧셈 기법 : 계절성 요소가 전체 데이터에서 일정한 폭으로 나타날 때 이용
- 곱셈 기법 : 계절적 변동폭이 데이터의 수준에 비례해 나타날 때
(이중 지수 평활법) 홀트 기법 : 시계열 데이터를 실질적인 값인 수준 요소와 추세, 두 가지 요소로 분리
(삼중 지수 평활법) 홀트 - 윈터스 계절성 기법 : 계절성을 표현하는 새로운 평활 매개변수 감마가 추가됨
# 이중 지수 평활법 (홀트 기법)
from statsmodels.tsa.holtwinters import ExponentialSmoothing
# 덧셈 기법
airline['DES_add_12'] = ExponentialSmoothing(airline['Thousands of Passengers'], trend = 'add').fit().fittedvalues.shift(-1)
# 곱셈 기법
airline['DES_mul_12'] = ExponentialSmoothing(airline['Thousands of Passengers'], trend = 'mul').fit().fittedvalues.shift(-1)
# 삼중 지수 평활법 (홀트-윈터스 기법) / 추가적인 인자가 있어서 shift(-1)이 불필요
airline['TES_mul_12'] = ExponentialSmoothing(airline['Thousands of Passengers'], trend ='mul',seasonal = 'mul', seasonal_periods = 12 ).fit().fittedvalues

일반 예측 모델
* 일반 예측 과정의 단계
1. 데이터를 기반으로 모델을 선택하는 것
2. 훈련/테스트 셋 나누기
- 테스트 데이터셋의 크기는 예측하고자 하는 기간의 크기보다는 커야 한다.
- 그러나 예측하고자 하는 기간이 길수록 더 많은 예측을 수행하면서 그만큼 노이즈가 추가되고 예측을 기반으로 또 예측을 하게 되므로, 예측의 정확도가 낮아진다.
3. 훈련 데이터셋에 모델을 피팅
4. 테스트셋으로 모델 평가
5. 모델에 만족하면, 모델을 전체 데이터셋에 피팅한 후 실제 미래를 예측
# 앞으로
다음 주부터는 오프라인으로 태블로 수업을 듣는다.
조별로 하는 것이라, 매일 과제도 있고 조금 빡세다고 하지만 오히려 강제성이 생겨서 더 좋을 거 같다는 생각이 든다.
* 유데미 큐레이션 바로가기 : https://bit.ly/3HRWeVL
* STARTERS 취업 부트캠프 공식 블로그 : https://blog.naver.com/udemy-wjtb
본 후기는 유데미-웅진씽크빅 취업 부트캠프 4기 데이터분석/시각화 학습 일지 리뷰로 작성되었습니다.
'유데미 스타터스' 카테고리의 다른 글
| 유데미 스타터스 취업 부트캠프 4기 - 데이터분석/시각화(태블로) 7주차 학습일지 (1) | 2023.03.26 |
|---|---|
| 유데미 스타터스 취업 부트캠프 4기 - 데이터분석/시각화(태블로) 6주차 학습일지 (0) | 2023.03.19 |
| 유데미 스타터스 취업 부트캠프 4기 - 데이터분석/시각화(태블로) 4주차 학습 일지 (1) | 2023.03.05 |
| 유데미 스타터스 취업 부트캠프 4기 - 데이터분석/시각화(태블로) 3주차 학습 일지 (0) | 2023.02.26 |
| 유데미 스타터스 취업 부트캠프 4기 - 데이터분석/시각화(태블로) 2주차 학습 일지 (0) | 2023.02.19 |
